In structural finite element analysis, non-metal materials such as rubber and biological tissues are often encountered. Because the mechanical properties of these materials are very different from the mechanical properties of metal materials, such as large elastic deformation, incompressibility, viscoelasticity, etc. Researchers and engineers classify these materials as hyperelastic materials, and group the mechanical models that describe such materials as hyperelastic models.
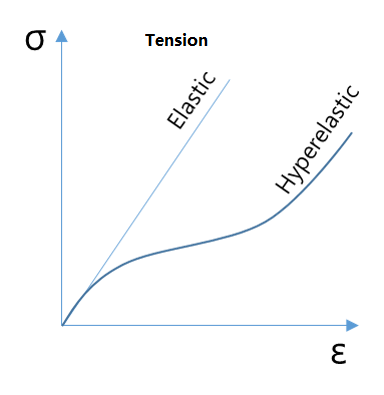
These hyperelastic materials (models) have the following significant characteristics:
- Can withstand large elastic (recoverable) deformation, sometimes with stretch up to 1000%.
- Hyperelastic materials are almost incompressible. Because the deformation is caused by the straightening of the molecular chain of the material, the volume change under the applied stress is small.
- The stress-strain relationship is highly nonlinear. Normally, the material softens first and then hardens under tension, but hardens sharply when compressed.
To predict and analyze the mechanical properties of these hyperelastic materials, many models have been proposed. Common hyper-elastic models are Neo-Hookean, Mooney-Rivlin, Odgen, Arruda-Boyce, Gent, Yeoh, Blatz-Ko, etc. At present, these models are widely used in many fields including rubber products (such as rubber seals), biological materials (such as muscles), and computer graphics in filming. WELSIM has also supported these models. In this article, we will be discussing the neo-Hookean in detail.
Neo-Hookean model
Proposed by Ronald Rivlin (1915–2005) in 1948, Dr. Rivlin is also well-known for the Mooney-Rivlin hyper-elastic model. It can be seen that neo-Hookean is not a model named after a person. This British-American physicist studied physics and mathematics at St John’s College, Cambridge, being awarded a BA in 1937 and a ScD in 1952. He worked for the General Electric Company, then the UK Ministry of Aircraft Production, then the British Rubber Producers Research Association. He later moved to the United States and taught at Brown University and Lehigh University.
The Neo-Hookean model is the simplest form of all commonly used hyper-elastic models. The elastic strain energy potential energy is expressed as
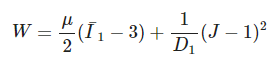
Where u is the initial shear modulus. D1 is the material’s incompressible parameter. It can be found that the model is a strain energy function based on the strain tensor invariant I_1. If the material is assumed to be incompressible, J = 1 and the second term becomes zero.
The Neo-Hookean model is derived based on classic statistical thermodynamic results. This is similar to the Arruda-Boyce model we discussed in the last article. When the limiting network stretch parameter in the Arruda-Boyce model becomes infinite, it is equivalent to neo-Hookean. At the same time, this model can be regarded as a special form of the Polynomial model. For polynomial model parameters N = 1 and C01 = 0, the polynomial model is equivalent to neo-Hookean.
The Neo-Hookean model has a constant shear module. Generally, it is only suitable for predicting the mechanical behavior of rubber with uniaxial tension of 30% to 40% and pure shear of 80% to 90%. While it is not very accurate to predict the large strain deformation. Although this model is not as versatile as other models, especially for large strain or tensile conditions. The neo-Hookean model has the following advantages:
(1) Simple. There are only 2 input parameters. If the material is assumed to be incompressible, then only one parameter is required: the initial shear modulus. Since only one parameter is needed from the test data, the number of required tests is small.
(2) Compatible. The material parameter obtained from one type of deformation stress-strain curve can be used to predict other types of deformation. Especially for the small and medium strain conditions.
It is worth mentioning that neo-Hookean is not only applied to science and engineering but also used in the computer graphics in the filming industry because of its simplicity and physical-based solutions. As shown in the figure, the process of hand movement, the muscle and skin changes calculated using the neo-Hookean model appear extremely natural.

Neo-Hookean finite element analysis example
In the following section, we apply the neo-Hookean material in the finite element analysis software WELSIM to simulate the deformation of a soft tube under tension. We constrain one end of the tube and apply force on another side, and compute the deformation and stress.
Analysis steps:
(1) Set the unit system to Metric (kg-mm) and create a structural static analysis project.
(2) Set material properties.
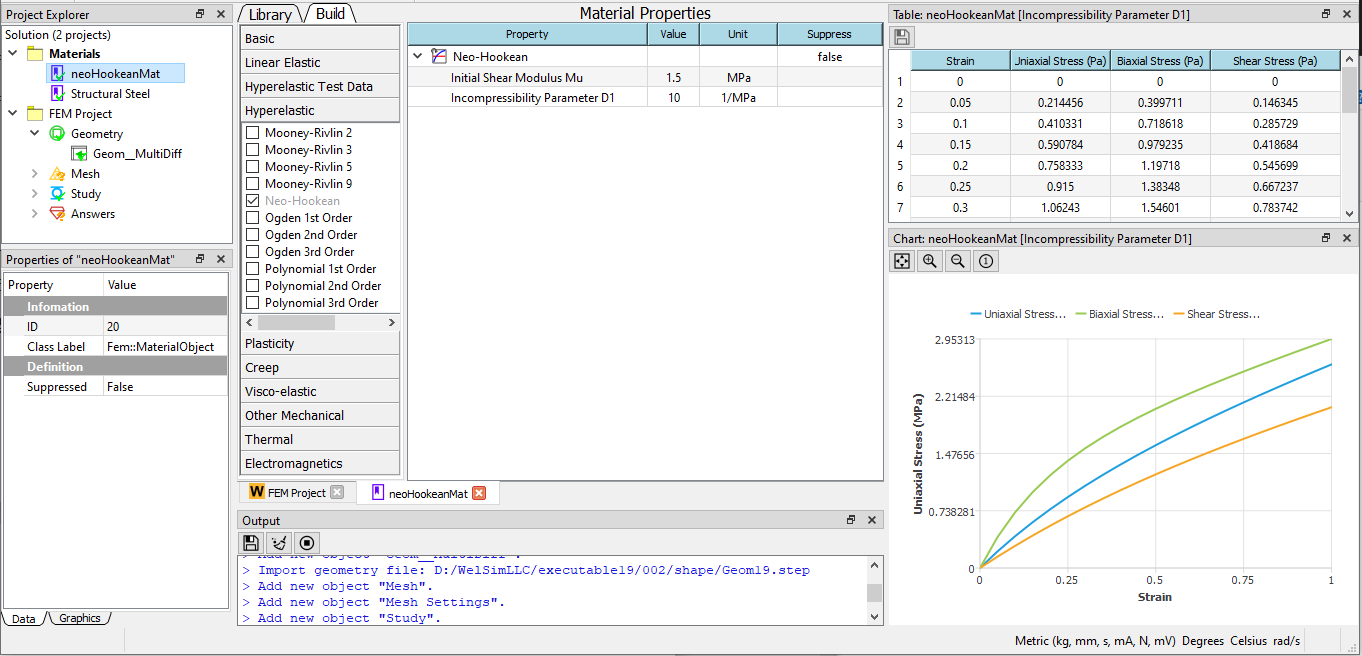
Create a new material. Double-click this material object to enter editing mode. Toggle the neo-Hookean property from the hyperelastic section in the toolbox. In the properties view, assign the values: Mu = 1.5 MPa, D1 = 10 MPa^-1. When the parameters are defined, the stress-strain curve of the corresponding model can be seen in the graph window. Press F2 on the material object and change the object name to neoHookeanMat.
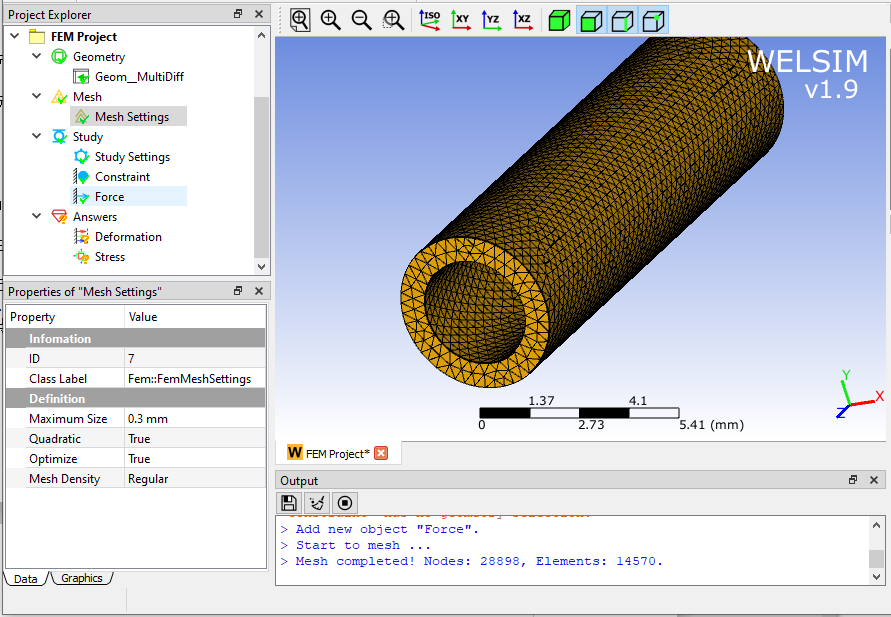
(3) Create a geometry The tube can be created by the boolean operation between two cylinders, with an inner diameter of 3mm, an outer diameter of 4.4mm, and a length of 15mm.
(4) Generate mesh: Set the maximum element size to 0.3 mm and use higher-order elements. After meshing, we obtain 28,898 nodes and 14,570 Tet10 elements.
(5) Boundary conditions Impose a fixed constraint on one end of the tube. A horizontal force in the Z direction is applied to another end of the tube with the magnitude 1N.
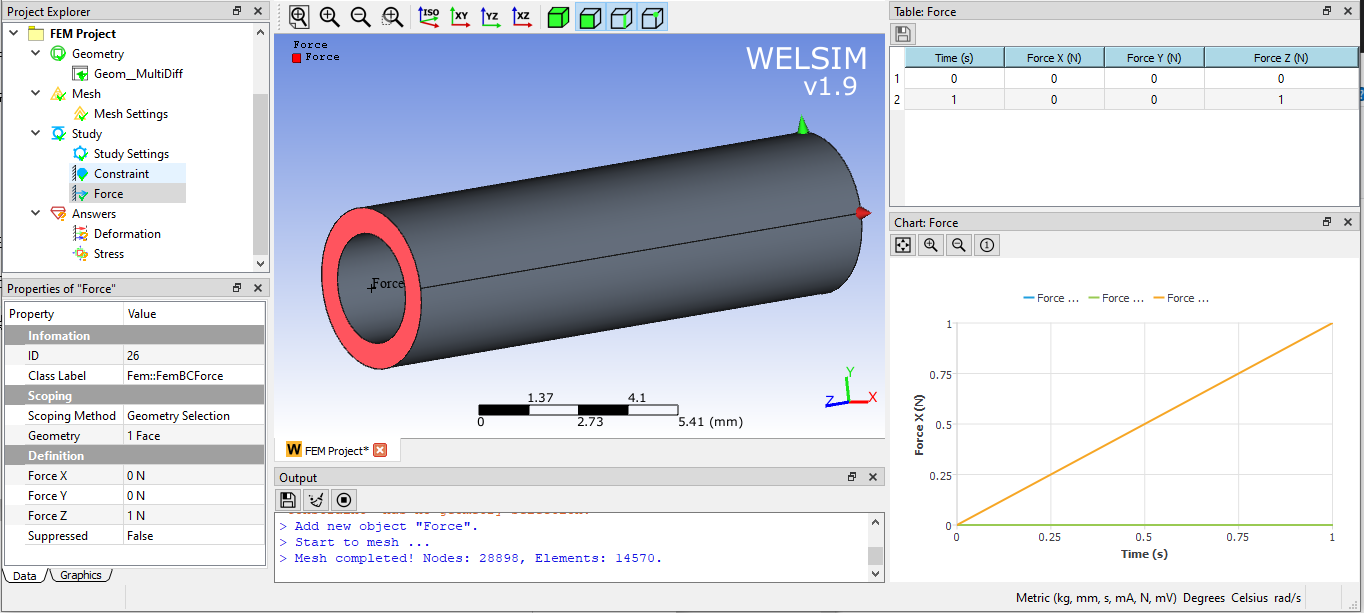
(6) Set model, solve and evaluate results. For better convergence, we set three substeps. Click the solve button, the solution will be calculated quickly. The deformation on Z direction and von-Mises stress are shown in the figures below.
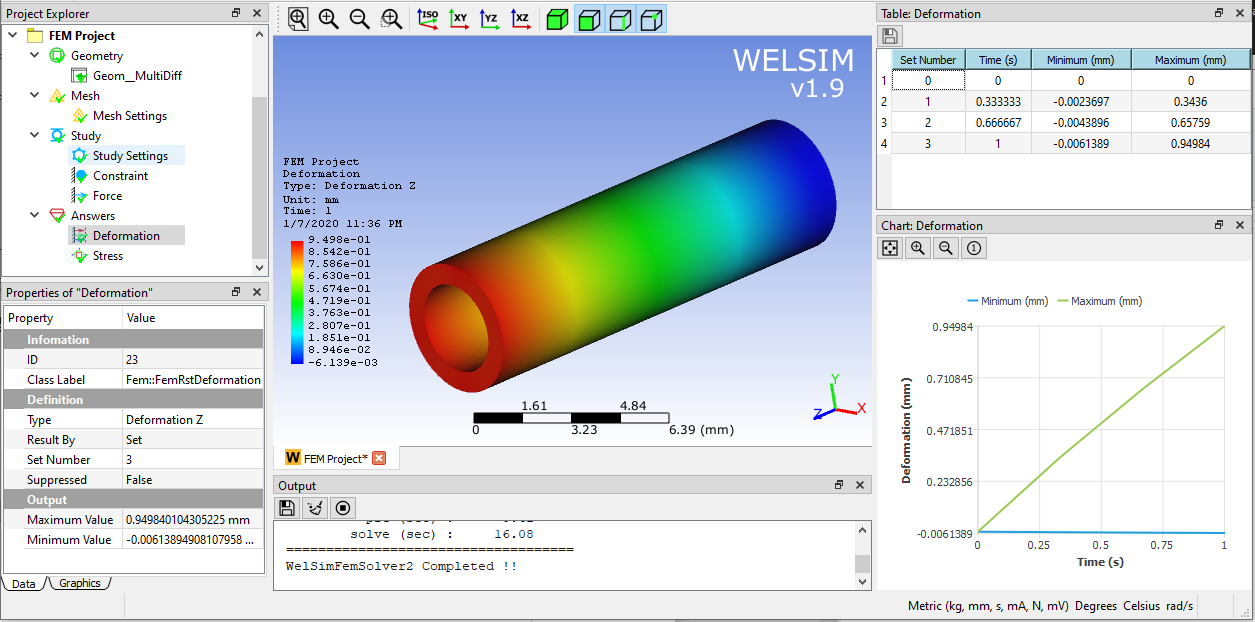

The maximum Von-Mises stress occurs at the fixed area of the tube, and the magnitude is 0.63 MPa.
Before the advent of finite element software, the calculation and prediction of material nonlinearities were complicated and time-consuming. Now with finite element software, the analysis of nonlinear materials has become faster, more accurate and more fun.