In previous articles, we have introduced the hyperelastic model in nonlinear finite element analysis, and also introduced the well-known Arruda-Boyce and neo-Hookean models in detail. Today we will be discussing another famous hyperelastic model: Mooney-Rivlin.
Mooney-Rivlin is named after the surname combination of two physicists, M. Mooney and R. S. Rivlin. In 1940, Mooney published a paper entitled “A theory of large elastic deformation” in the Journal of Applied Physics. Eight years later, in 1948, Rivlin published a paper “Large elastic deformations of isotropic materials” in Philosophical Transactions of the Royal Society of London. Those two papers build the essence of the Mooney-Rivlin hyperelastic model, which has dominated the rubber mechanics for about half-century. At the same time, it also lays the foundation for other models based on strain tensor invariants. Another type of hyperelastic model is based on principal stretches, such as the Ogden model, which we will discuss in the future.

Mooney was born in Kansas City, Missouri, the USA in 1893. He received an undergraduate degree from the University of Missouri at the age of 24 and a Ph.D. at 30. He was a fellow of the National Research Council and a physicist at Western Electric and American Rubber Company. Like Rivlin we introduced earlier, Dr. Mooney devoted his life’s work and research to the mechanics of polymer materials. Mooney is more than 20 years older than Rivlin. Dr. Rivlin has been introduced in the last article, so we won’t repeat it here.
Like other hyperelastic models, we use elastic strain energy to characterize mechanical properties. Mooney-Rivlin is based on the order of the level, there are four types: two-parameter, three-parameter, five-parameters, and nine-parameter strain energy.
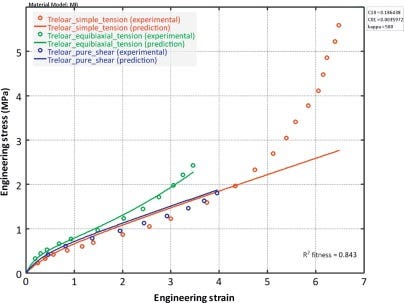
The form of the strain-energy potential for a two-parameter Mooney-Rivlin model is:
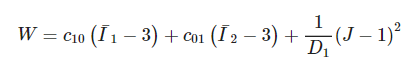
The form of the strain-energy potential for a three-parameter Mooney-Rivlin model is:
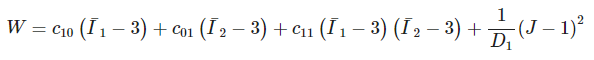
The form of the strain-energy potential for a five-parameter Mooney-Rivlin model is:
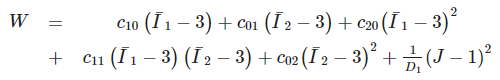
The form of the strain-energy potential for a nine-parameter Mooney-Rivlin model is:

From these four potentials, we can tell:
- The higher-order potential can model more complex strain-stress constitutive relations but requires more computational efforts, experimental data, and parameter fitting. At the same time, as the nonlinearity becomes stronger, the higher-order may be difficult to converge.
- Mooney-Rivlin model is a special form of Polynomial model. When N = 1, the Polynomial model is reduced to 2-parameter Mooney-Rivlin; when N = 2, the Polynomial model is reduced to 5-parameter Mooney-Rivlin; when N = 3, the Polynomial model is reduced to 9-parameter Mooney-Rivlin.
- The 2-parameter Mooney-Rivlin has the following features: it is reduced to Neo-Hookean when parameter C01=0. (shear module u=2*C10 ). The non-zero C01 term makes the model under uniaxial tension more accurate, but it still cannot accurately simulate the multiaxial stress states. The parameter obtained from one type of deformation experiments, cant not predict another type of deformation accurately. Since the shear modulus of 2-parameter Mooney-Rivlin is constant (u=C10+C01), it cannot model the carbon black rubber. The summation of C10 and C01 must be positive. For most rubber materials, the ratio of C10 / C01 lies between 0.1 and 0.2.
- Three- or more-parameter Mooney-Rivlin models can describe unsteady shear modulus. However, solutions need to be carefully evaluated when the high-order terms are introduced, as it may produce unstable strain energy values and yield non-physical solutions.
Selection and positive definiteness of strain energy potential
Which of these four Mooney-Rivlin models should be used in a practical simulation? It is often determined from the strain-stress curve of material experiments. For single curvature (no inflection point) stress-strain curve, 2 or 3 parameters can be used. Double curvature (including an inflection point) can use 5 parameters. For three curvatures (including 2 inflection points), a 9-parameter model can be selected.
At the same time, to produce effective and correct superelastic material properties, Mooney-Rivlin parameters must meet certain positive definiteness requirements. Failure to meet these conditions may cause a converge difficulty. For Mooney-Rivlin with different numbers of parameters, the requirement of positive definiteness is shown in the figure.

Overall, the Mooney-Rivlin model has been widely recognized and applied. Especially in the small and medium strain applications (0 ~ 100% tensile and 30% compression), Mooney-Rivlin can precisely characterize the mechanical behavior of rubber materials. Four types of potentials also provide users with more choices to model various material behaviors. However, Mooney-Rivlin has some limitations:
- Not suitable for the deformation that exceeds 150%.
- Because higher-order Mooney-Rivlin has many parameters, the parameters are relatively difficult to obtain from the manual or literature, which needs curve fitting of experimental data.
- Not suitable for the analysis of compressible hyperelastic materials, such as foam.
- The error could be large when the strain/stress is beyond the range of input experimental data.
An example of Mooney-Rivlin hyperelastic analysis
In this example, we will use a 5-parameter Mooney-Rivlin to analyze the compression state of a rubber cylinder.
Define a Mooney-Rivlin hyperelastic material
Here we define the rubber material and input the parameters as: C10 = -0.55 MPa, C01 = 0.7 MPa, C20 = 1.7 MPa, C11 = 2.5 MPa, C02 = -0.9 MPa, D1 = 0.001 MPa^-1.
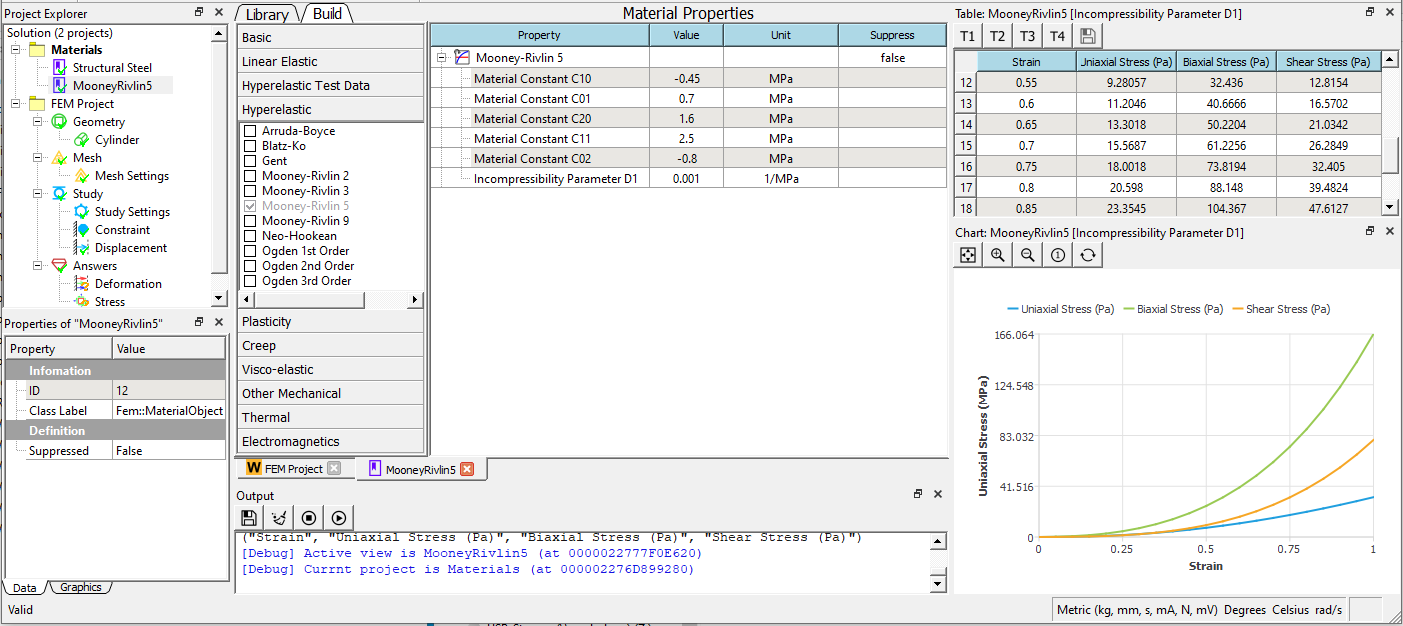
Modeling
Create a cylinder with a diameter of 10 mm and a height of 10 mm. Meshing. Fixed bottom constraint. A 5mm downward displacement is applied onto the top surface.
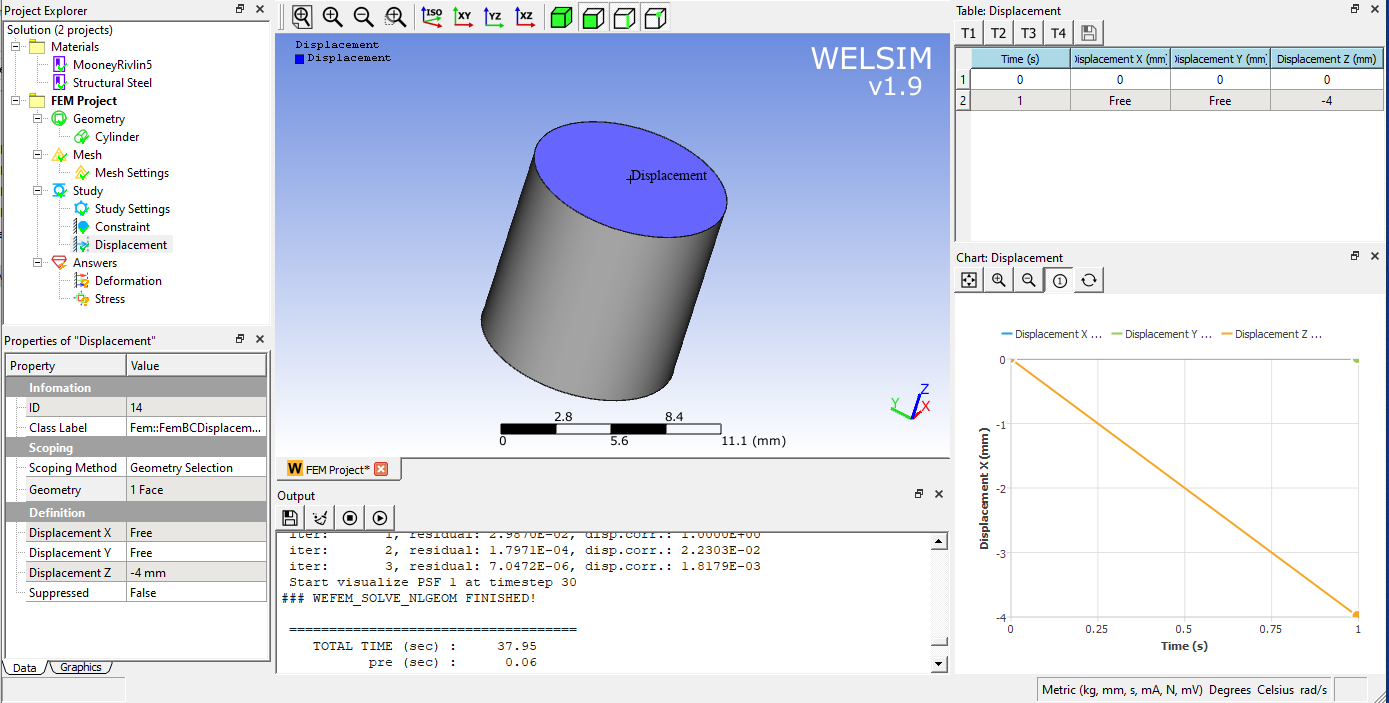
Solve
Since it is a nonlinear analysis, we set 30 substeps for easier convergence. And click the solve button.
View Results
The equivalent stress distribution is shown in the figure. It can be found that the von-Mises stress increases in a nonlinear manner.
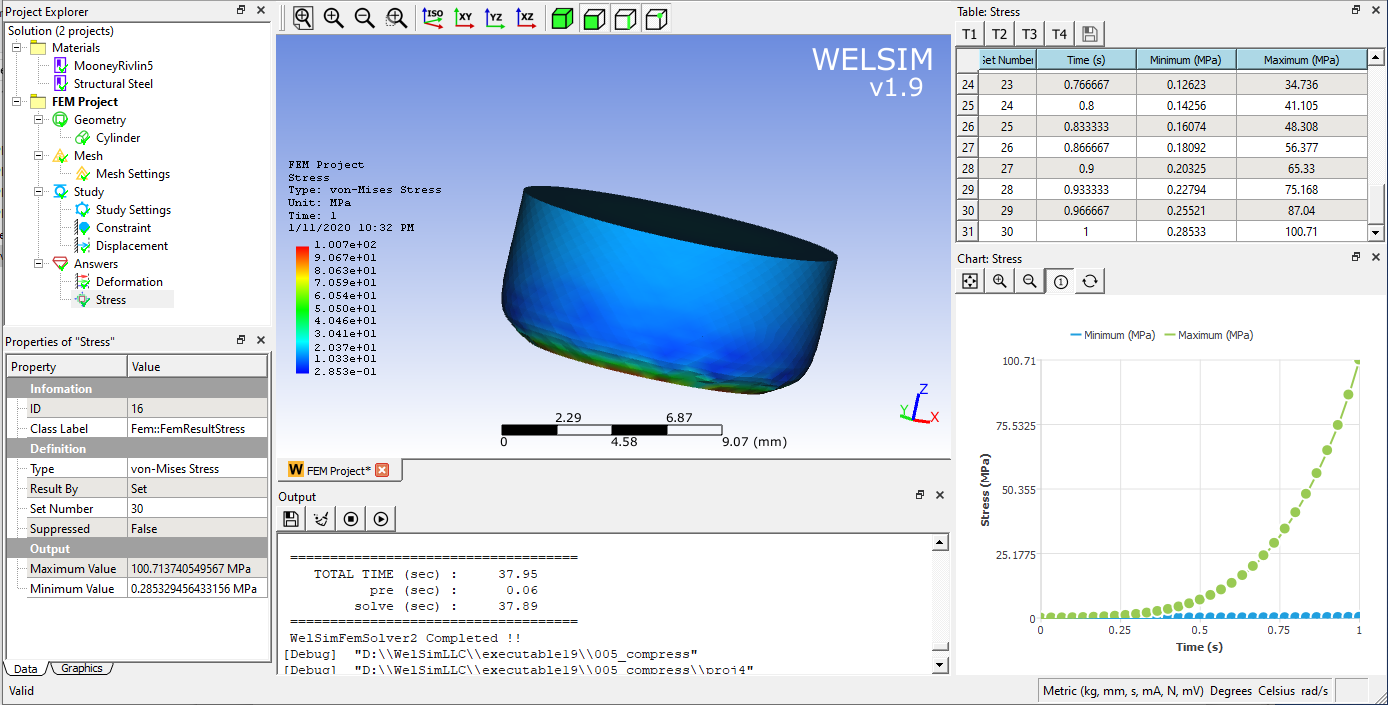
Overview of Chia plotting and farming
The Chia project is based on proofs of space and time, a brand new Nakamoto consensus allowing for underutilized storage capacity to secure the blockchain. Proofs of space are stored in plot files, where a commonly used k=32 plot is 101.3GiB (108.8 GB, or Gigabytes). Generating plot files is a process called plotting, which requires temporary storage space, compute and memory to create, sort, and compress the data into the final file. This process takes an estimated 256.6GB of temporary space, very commonly stored on SSDs to speed up the process, and approximately 1.3TiB of writes during the creation. The community realized early on that guidance was needed for SSD endurance, and a wiki was created to help users select the proper SSD for plotting.
SSD Market and Endurance
The new Chia cryptocurrency has received some inquiries regarding accelerated wear-out on SSDs. Solid-state drives are the standard for storing user data in current laptops and desktops, overtaking HDDs due to lower latency, lower power, improved battery life, smaller form factors, and better reliability than hard disk drives. The worldwide SSD market reached $33.2B [1], with consumer SSDs reaching 338M units and $17.6B [2] in 2020 alone. SSDs come in a large variety. SSDs segmentation occurs with different segments (consumer, datacenter, enterprise), interfaces (PCIe/NVMe, SATA, SAS), performance, endurance, and media type (MLC, TLC, QLC) for the 3D NAND technologies. Mainstream SSDs use 3D NAND flash non-volatile memory in the floating gate and charge-trap / replacement gate technology (major NAND vendors include Micron, Intel, Samsung V-NAND, Kioxia & WD BiCS). 3D NAND has a limited amount of write endurance or the amount of data written to a drive before wearing out (device failure or inability to read or write additional user data). SSDs are rated in TBW (terabytes written) or DWPD (drive writes per day) to show how much data can be written before wearing out. [3] SSD vendors use the JESD219 spec from the JEDEC organization [5] for this rating with standardized tests and reporting. Endurance is very well understood and can be accurately modeled and predicted. [7]
Chia plotting process and SSD selection
Chia plotting creates the cryptographic data stored later for the proofs of space (retrieved later to validate the network in a process called farming). Plotting is only required once upon creating the data and requires compute, memory, and ephemeral storage. Plotting is a write-intensive process due to creating random data, sorting, and compression. The Chia team and community advocate using data center class SSDs or consumer drives meant for high-end desktops and workstations with a high TBW endurance rating for the plotting process. If a user selects a high-endurance data center SSD, they can plot for up to 10 years [4] before wearing out the device during the plotting process. Consumer SSDs have been optimized for light client workloads (web browsing, office work, gaming) and are not suitable for Chia plotting. With the endurance requirements being more significant than average consumer SSDs, the consensus in the community is to avoid using these if possible for Chia plotting. The Chia team realizes that consumer SSDs are the ones that are generally available, and there are some models that have enough endurance where users can plot all the farming capacity they have and still have a surplus of endurance. A comparison using a device not designed for such a workload would not be an accurate representation of what is being used to plot in Chia.
Also don't clean nonstick pans with steel wool, don't clean vegetables with soap, and don't use your phone as a doorstop. These aren't arguments against steel wool, soap, or phones, they're basic guidelines about using your tools properly.
— Bram Cohen (@bramcohen) May 16, 2021
HDD Plotting
While most users are selecting SSDs [8] for Chia plotting to create the data faster and gain a competitive advantage, the software itself does run fine plotting directly to HDD, albeit slower. Mainstream HDDs are rated at 200-550TB/year workload to meet the reliability metrics on the specification sheet. A new hard drive being plotted directly to will likely be right up against this limit in the first year, but Chia farming is a write-once / read-many workload where writing additional data overtime is unnecessary. The farming process is lightweight and slight wear and tear on the drive once the drive is full of the plots needed to participate in the network.
Other case studies for selecting the wrong flash device based on endurance requirements.
Tesla performed a voluntary recall [6] after users reported MCU (Media Control Unit) failures. The root cause was the eMMC flash storage onboard not having enough write endurance to handle the logging that was being performed on the device. Calculating endurance is a very common prerequisite for determining the right fit for SSDs in any application. Thus, this was a good case study on the negative outcome of not understanding NAND flash’s endurance requirements.
Macbooks that use the new Apple M1 chip saw users reporting accelerated SSD wear out, [9] possibly due to the increased use of swapping in MacOS and Rosetta 2.
Questions or concerns, and note for SSD vendors
Please reach out to Jonmichael Hands, VP of Storage Business Development, if you are an SSD vendor, partner, cloud provider, or have any Chia and storage use questions. Send and email to [email protected] to get connected.
[1] Worldwide Solid State Drive Market Shares, 2020: Pandemic Drives Strong Growth for Enterprise and Client SSDs
[2] Forward Insights, Q1'21
[3] https://www.snia.org/forums/cmsi/ssd-endurance
[4] https://github.com/Chia-Network/chia-blockchain/wiki/SSD-Endurance
[5] https://www.jedec.org/
[6] https://www.tesla.com/support/8gb-emmc-recall-frequently-asked-questions
[7] http://intel.com/endurance
[8] https://github.com/Chia-Network/chia-blockchain/wiki/Reference-Plotting-Hardware
[9] https://www.macworld.com/article/338844/how-worried-should-you-be-about-your-m1-macs-ssd-lifespan.html