Previously, we discussed the Arruda-Boyce, neo-Hookean, and Mooney-Rivlin models. In this article, we will be talking about the Yeoh hyperelastic model, also called the Reduced Polynomial model. Yeoh model is anther hyperelastic model named after a person’s surface name, to thank Oon Hock Yeoh for his contribution to the rubber mechanics.
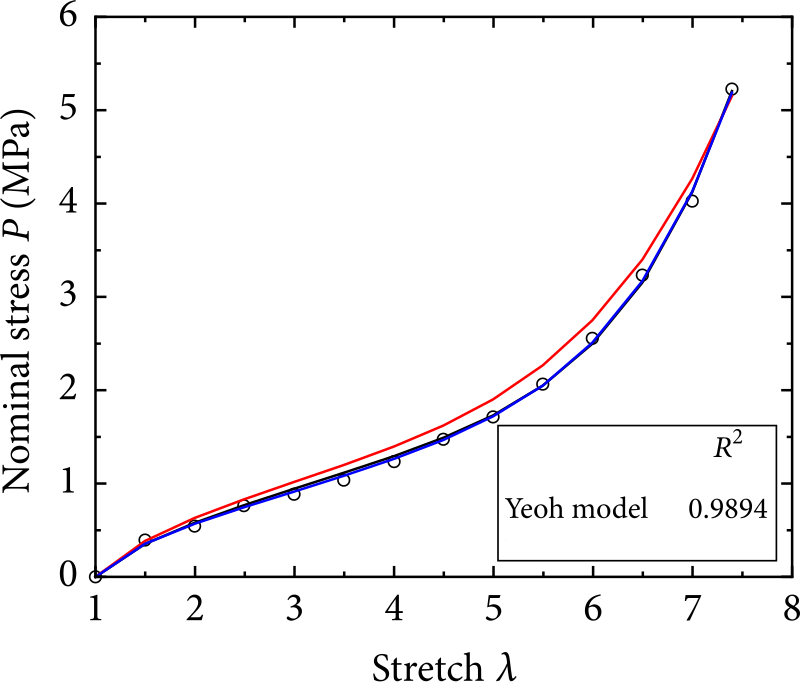
In 1990, Yeoh noted in investigations on a black-filled rubber that the material showed a significant decrease of shear modulus at low strains. Later he observed the same phenomena in unfilled rubber. Yeoh proposed to consider the observation in the hyperelastic model by adding an exponentially decaying term to the strain energy density of the model today known as the Yeoh model. He published the paper “Some forms of the strain energy function for rubber” in the journal “Rubber Chemistry and technology” to describe this theory. WELSIM already supports the Yeoh model.

There is no much information that can be found online about Oon Hock Yeoh himself. Yeoh now is an engineering Fellow of Freudenberg-NOK Sealing Technology Company in the United States. Previously he held various research positions at MRPRA (England), RRIM (Malaysia) University of Akron, GenCorp Research, and Lord Corporation. His publications include papers on hyper-elastic material models, finite element analysis and fracture mechanics. Like physicists Mooney and Rivlin, they are all mechanics in the industry who are engaged in rubber research.
Similar to other hyperelastic models, we use the strain energy potential to describe this model. The strain-energy potential of the Yeoh model is:
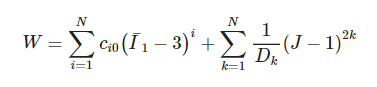
where J is the volume ratio after and before deformation. For incompressible materials, J = 1. I1 is the first invariant of Cauchy-Green strain tensor. N, Ci0 and Di are input parameters. It can be seen from the strain energy function:
- Yeoh and Mooney-Rivlin are very similar, both belong to the family of Polynomial model. In the same order, Yeoh is simpler than Mooney-Rivlin because it does not consider the role of the second invariant I2. However, the volumetric terms of the Yeoh are more complex than that of Mooney-Rivlin.
- The initial shear modulus is 2 * C10, and the initial modulus is 2 / D1. To ensure that the initial shear modulus is positive, the parameter C10 must be greater than zero.
- Although the order parameter N can be large, in practical applications, we only use at most 3 orders. When N = 1, Yeoh is equivalent to the neo-Hookean model. Therefore, it is generally recommended to use the third-order potential with N = 3, to take advantage of the superiority of the Yeoh model.
- When N> = 3, a typical inverse S-shaped rubber stress-strain curve can be described.
Pros:
- Simple and only a few parameters. The user only needs a small amount of experimental data to get reasonable numerical results, and the input parameters can be obtained only by the tensile experiment.
- Yeoh can describe a wide range of deformation. The reasonable results can be obtained under large uniaxial stretching and simple shear deformation.
- The higher-order potential can represent an inverse S-shape stress-strain curve and simulate the sharp rise of material stiffness at the later stage of deformation. The higher-order potential can model the carbon black filled rubber that shows non-constant shear modulus during deformation.
Cons:
- Predicting the deformation of biaxial tension may show some deviations.
- When dealing with complex deformation contains different types of strains. Yeoh may show inaccuracy.
- For small strain deformation, parameters need to be carefully chosen. There may be a deviation between the Yeoh model and the experimental data for small deformation. However, in the finite element analysis, this deviation is not serious, because the stress in the small strain region is small, and although the relative error may be large, the absolute error is small.
Nonlinear Finite Element Analysis of Yeoh Model
Select Yeoh 3rd order superelastic material and enter the parameters of carbon black filled rubber C10 = 0.57382 MPa, C20 = -7.4744e-2 MPa, C30 = 1.1321e-2 MPa, D1 = 0.01 MPa^-1, D2 = 0.1 MPa^-1, D3 = 0.5 MPa^-1.
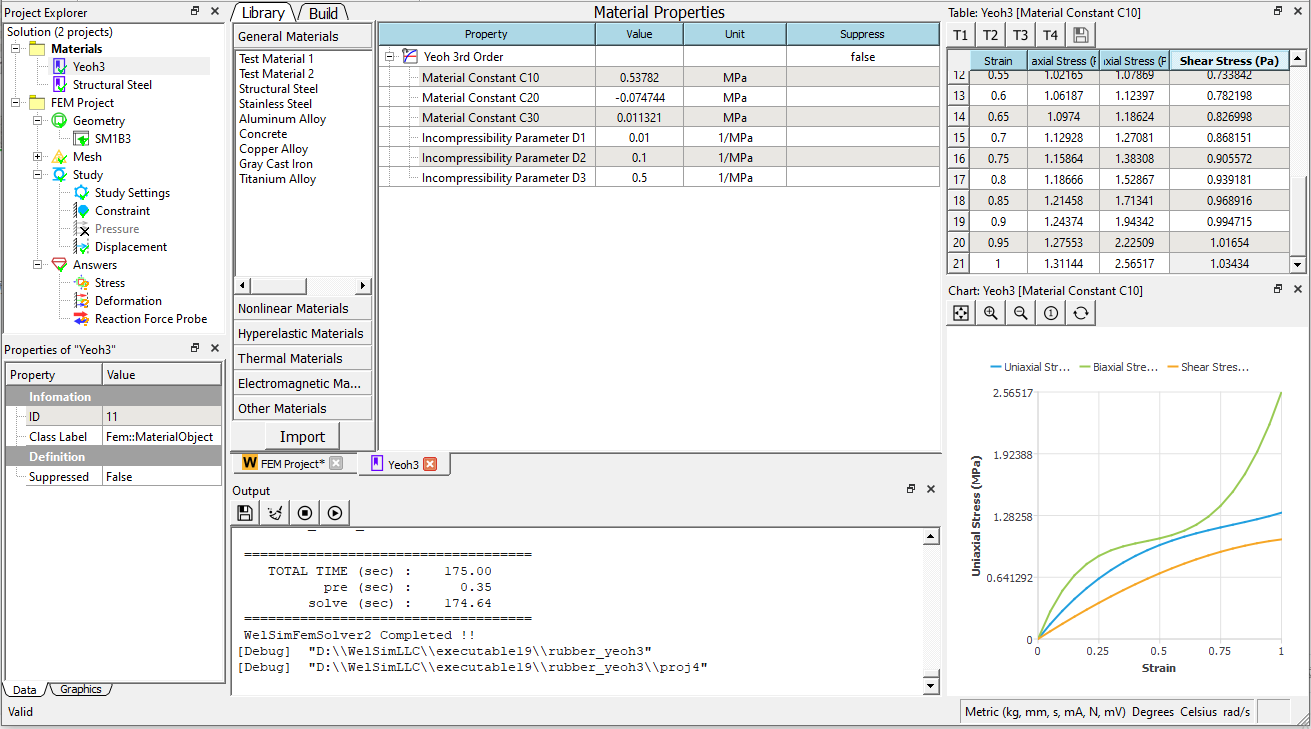
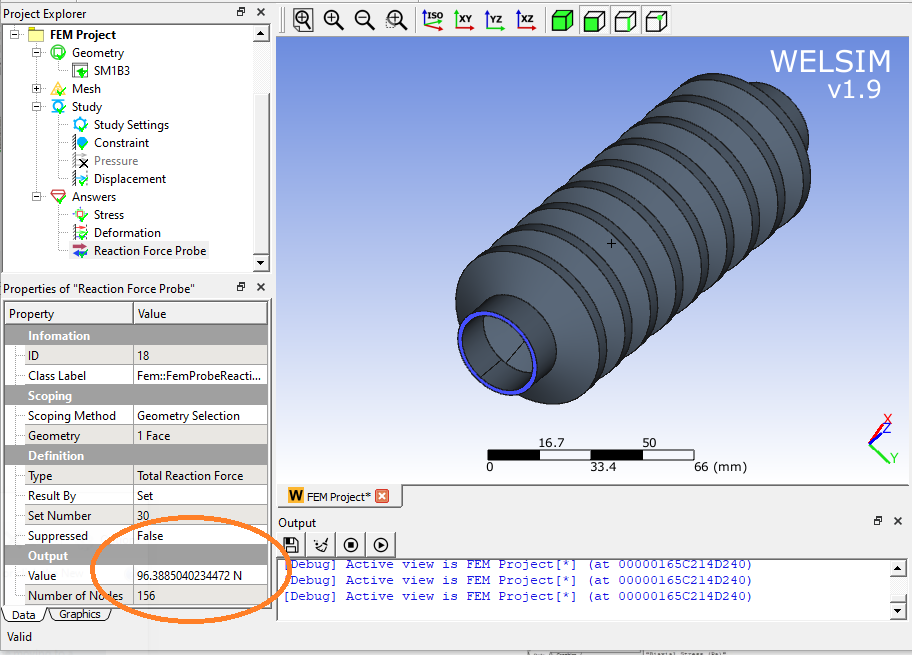
Import a rubber geometry, mesh it, constrain the bottom, and apply a 100mm upward displacement on the top.
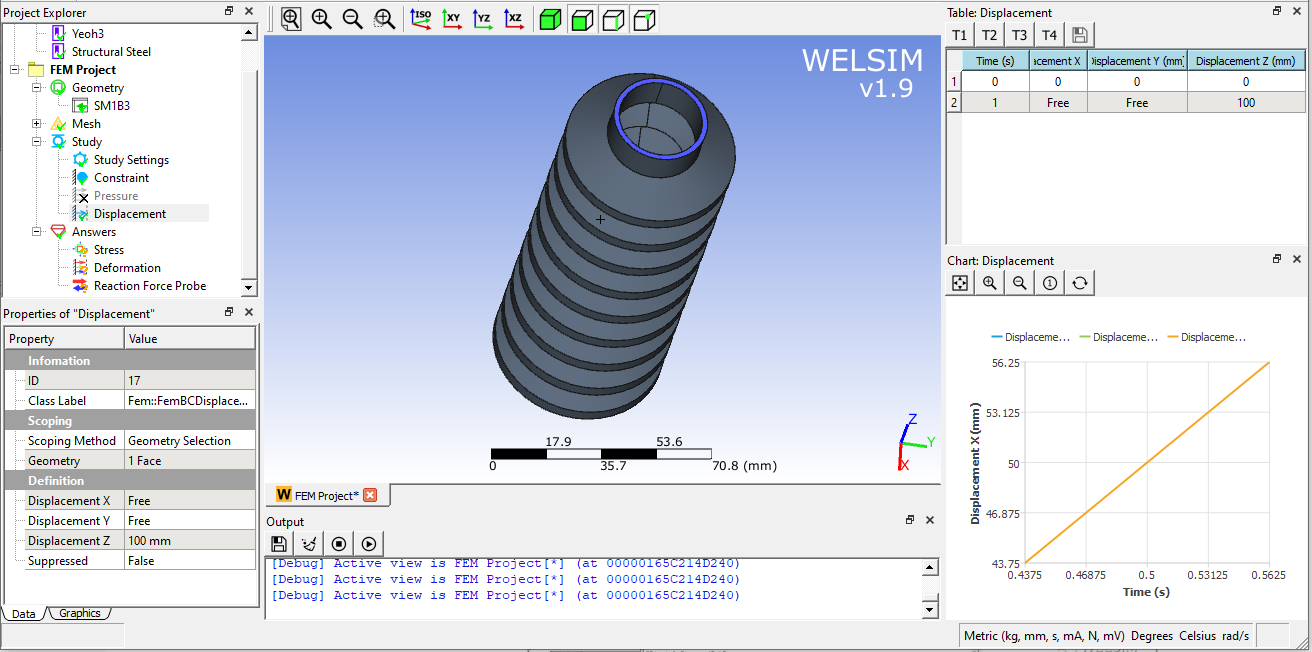
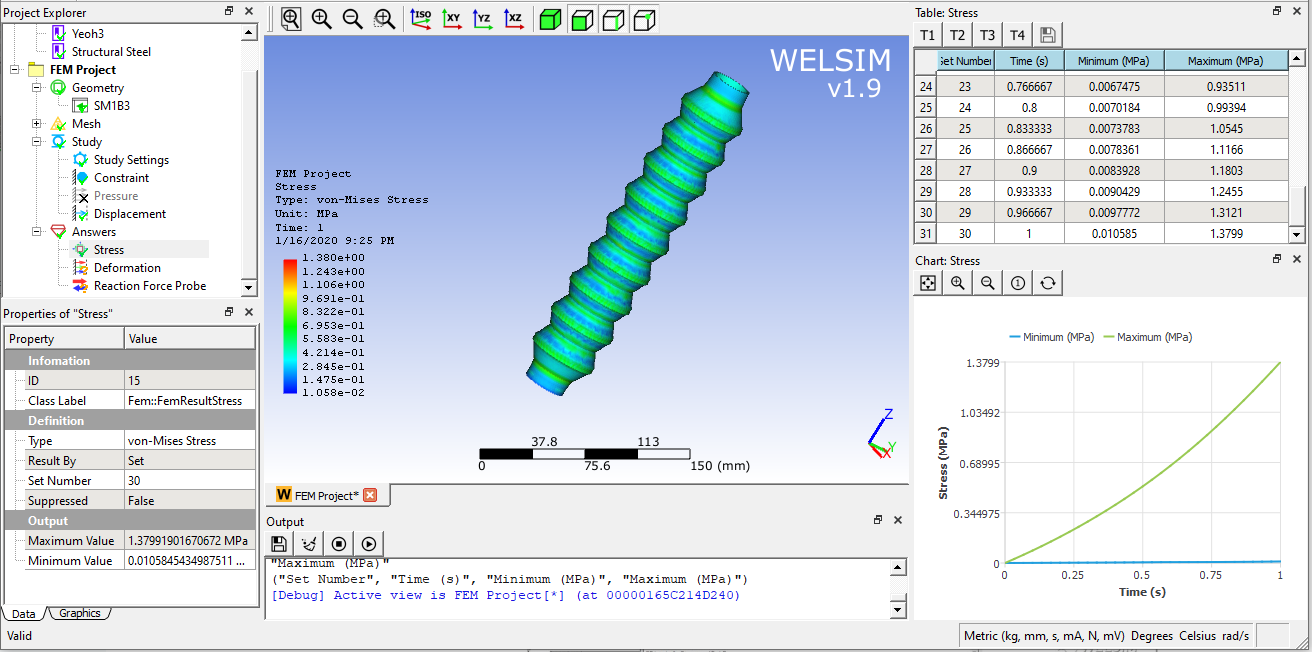
Solve and add a result object to display the contour of the von-Mises stress. The maximum stress vs time curve shows nonlinearity.
The reaction force at the bottom of the rubber structure is about 96.39 N.