In previous articles, we have introduced Arruda-Boyce, neo-Hookean, Mooney-Rivlin, Yeoh, Gent, Blatz-Ko and other hyperelastic models that often used in nonlinear finite element analysis. Now we will be discussing a special and widely applied hyperelastic model: Ogden. A versatile model that can be used for rubber, polymer, and biological tissues. The Ogden model has been successfully applied to the analysis of o-rings, seals and other industrial products. Its most special feature in the theoretical algorithm is that the principal stretches are used as the independent variable, rather than the strain tensor invariant. Like other hyperelastic models such as Mooney-Rivlin, Ogden hyperelastic model is named after Dr. Ogden, to thank his contributions to this hyperelastic model.
In 1972, Dr. Ogden, was a research fellow at the University of East Anglia, England, published a paper titled “Large Deformation Isotropic Elasticity: On the Correlation of Theory and Experiment for Compressible Rubber like Solids” in the journal “Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences”. This paper presents a detailed description of the mathematical and experimental basis of the Ogden and other hyperelastic models. The full text is clear, fluent, and pleasing to read. Ogden believes that expressing strain energy as a function of multiple independent strain invariants has, in general, the effect of complicating the associated mathematical analysis, particularly in calculating the instantaneous moduli of elasticity. He directly uses the principal stretches as the independent variable to construct the strain energy function, the proposed model is simple enough to be amenable to mathematical analysis, and adequate to represent the mechanical response of rubber-like solids. An excellent agreement between this theory and the experimental data is demonstrated also in the paper. Since both compressible and incompressible Ogden models share many similar characteristics, we only focus on the incompressible Ogden model here. The compressible Ogden will be introduced later. WELSIM already supports the Ogden model.

In 1943, Raymond William Ogden was born in the British. Between 1967 and 1970, he studied in the Ph.D. program at Cambridge University with guidance from professor Rodney Hill in the field of mechanics. His doctoral thesis was entitled “On Constitutive Relations for Elastic and Plastic Materials”. After graduating with a Ph.D. in 1970, he became a research fellow at the University of East Angela, England. Since 1984, Ogden has been a professor in the Department of Mathematics and Statistics at Glasgow University. We may have read his well-known book about nonlinear elasticity: “Nonlinear Elastic Deformations”. Ogden was elected to the Royal Society Follow in 2006. Unlike other nonlinear mechanics researchers who born in British, such as Rivlin and Gent, Ogden did not immigrate to the United States and has been engaged in research and education in British.
Strain-energy potential of Ogden model
The strain energy potential of the Ogden model is based on the principal stretches of the left Cauchy-Green strain tensor, which has the following form:
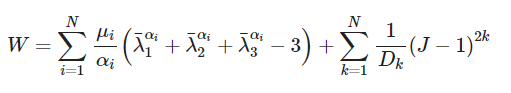
Where N is the order of the model, usually N takes a number between 1–3. u_i and a_i are material constants, where the unit of u_i is pressure, a_i is a dimensionless quantity, unitless. D_i is an incompressible parameter used to indicate volume change. The reduced principal stretches have the following relationship
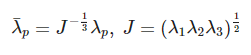
From this potential function we can know:
- The model uses the principal stretches λ1, λ2, and λ3 in the three directions of the strain tensor as variables.
- The initial shear modulus is u = sum (u_i * a_i) / 2. The initial bulk modulus is K = 2 / D_1.
- When N = 1, a1 = 2, it is equivalent to the neo-Hookean potential.
- When N = 2, a1 = 2, a2 = -2, the Ogden potential can be converted to the 2-parameter Mooney-Rivlin model.
- Since the principal stretches are the square root of the eigenvalue of the strain tensor, the eigenvalue of the 3x3 strain matrix needs to be calculated to obtain the material stiffness matrix and stress.
- The input material constant must satisfy u_i * a_i> 0 to ensure the stability of the algorithm.
Behaviors and limitations of the Ogden model
- Versatile. It can be widely used in various types of hyperelastic constitutive relations. The model results can be accurate for the entire strain range of rubber materials.
- Ideal for handling large strain problems. When N = 3 or higher, the required accuracy can be achieved even when the strain is as high as 700%.
- Suitable for describing non-constant shear modulus and slightly compressed material behavior.
- It can describe the rapid stiffness rise in the late stage of deformation.
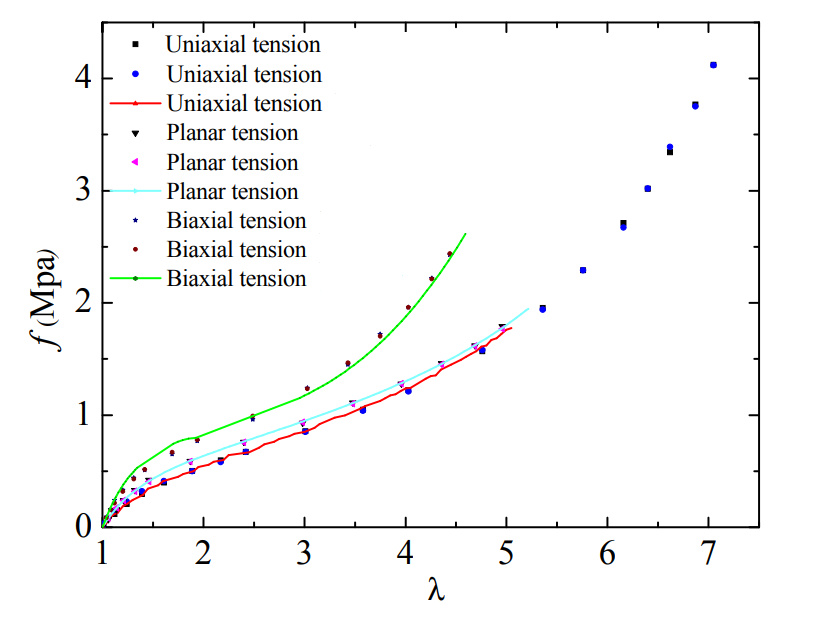
- The material parameters determined by one type of experiment cannot be used to predict another type of deformation. It is not recommended to use in the case of insufficient experimental data, such as only uniaxial tensile test data.
Nonlinear finite element analysis with Ogden model
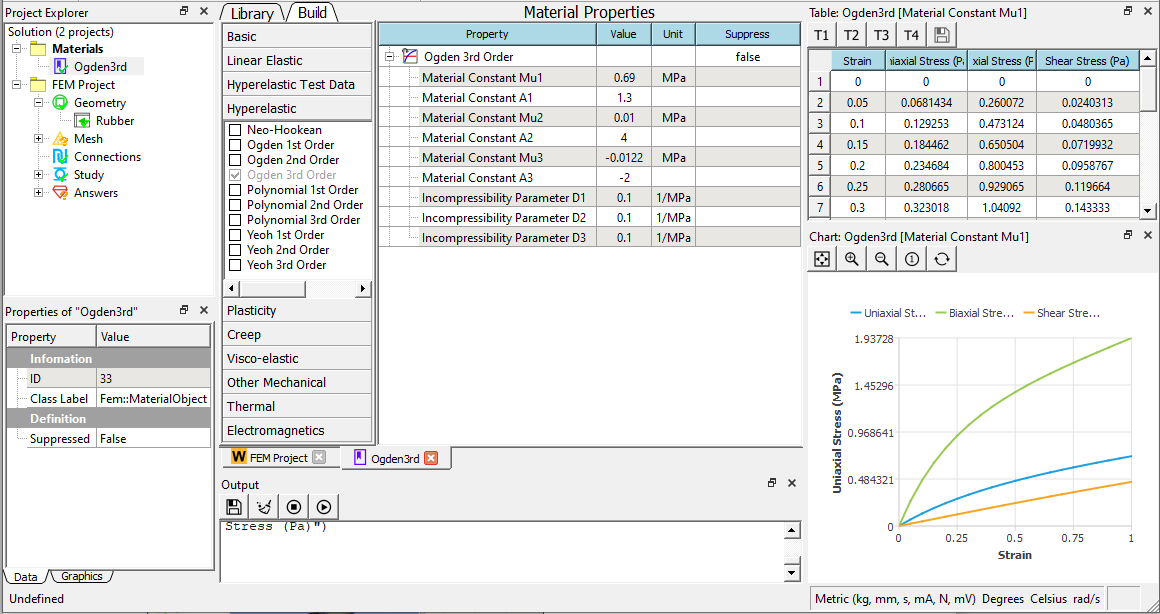
Define materials
Select Ogden 3rd order hyperelastic material and input parameters u1 = 0.69 MPa, a1 = 1.3, u2 = 0.01 MPa, a2 = 4.0, u3 = -0.0122, a3 = -2, D1 = 0.1 MPa^-1, D2 = 0.1 MPa^-1, D3 = 0.1 MPa^-1.
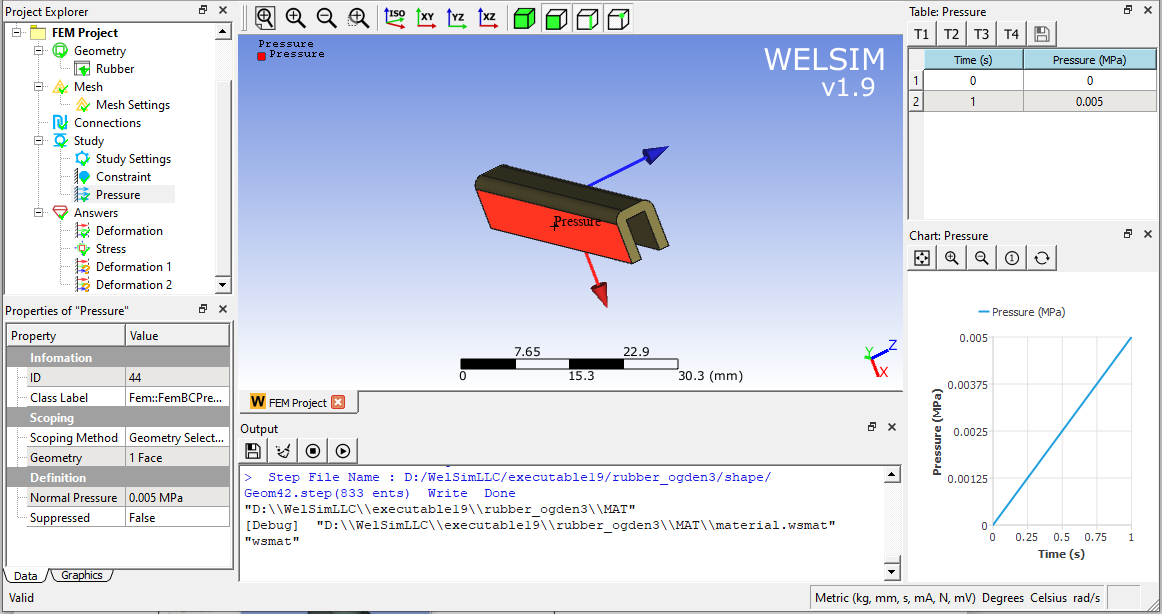
Import the rubber blade geometry, mesh it, and apply 5e-3 MPa positive pressure on the side.
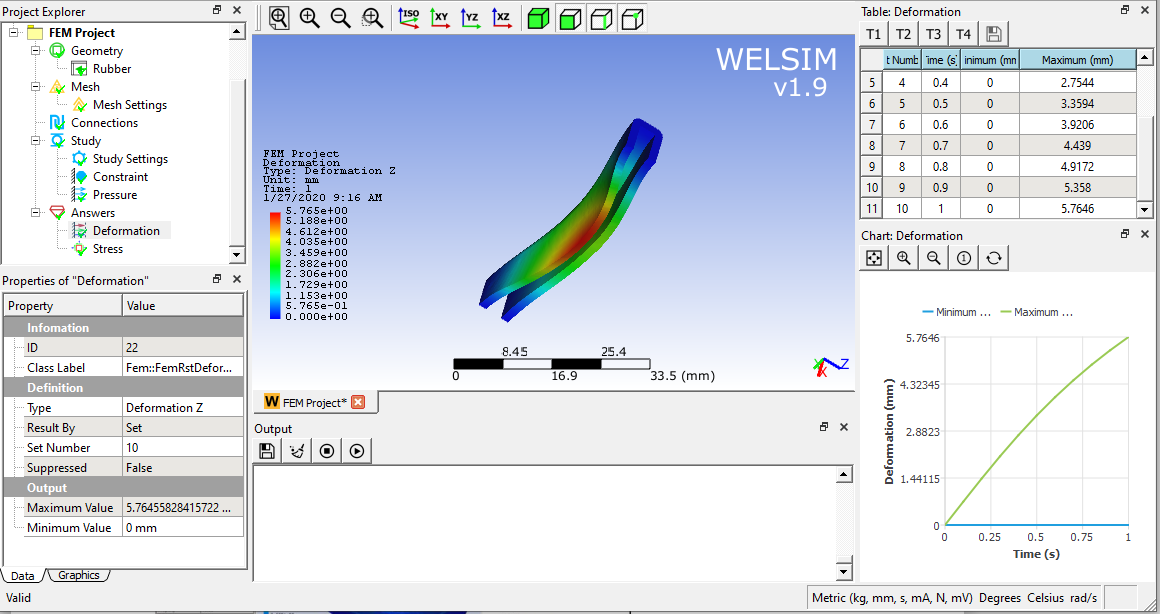
Solve and add the displacement result node to display the result contour and maximum and minimum values data. As shown in the figure below, the deformation in the Z direction is nonlinear to time.
In fact, from the perspective of practical finite element analysis, as long as the model can accurately express the mechanical properties of the rubber material with reasonable curve fitting coefficients, the form of strain energy function does not seem to be so significant whether it is expressed by the strain invariant or the principal stretches. The choice of model is mainly determined by the difficulty of coefficient fitting and the ability of nonlinear convergence.