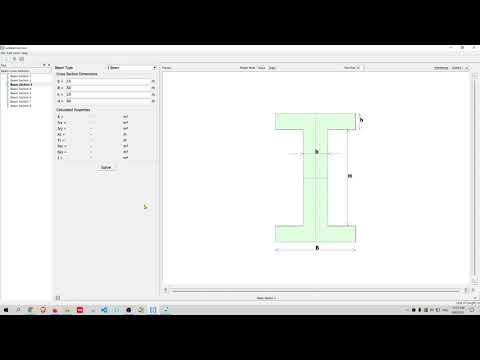
The beam is a specific structure commonly used in engineering. The beam can be made as an independent beam or can be combined with other structures such as plate, shell, or concrete solid structure to form an integral beam or multi-layer frame.

Due to the wide application of beams, the industry has also formed some standards. According to the different cross-sectional forms, we classify various beams as rectangle beam, T-beam, I-beam, C-beam, hollow rectangle beam, etc. According to the different forms of structural forces, it can be divided into simply supported beams, continuous beams, cantilever beams, main beams, and secondary beams.
When using beam structures in engineering, scientific calculations must be made according to the cross-section and force conditions to comply with relevant safety regulations. Although some manuals have provided the relevant parameters of beam cross-sections, it takes time to look up and not all types of cross-sections are covered. A simple and easy-to-use cross-section calculation software has many practical uses. At the same time, in the finite element analysis, the relevant properties of the cross-section are also necessary for the beam element.
BeamSection is a simple and easy-to-use beam cross-section calculation software. Provides common beams in engineering and related calculation results.
Let’s demonstrate how to use BeamSection to quickly obtain the relevant properties of the beam cross-section.
- Open BeamSection and create a new beam section object.
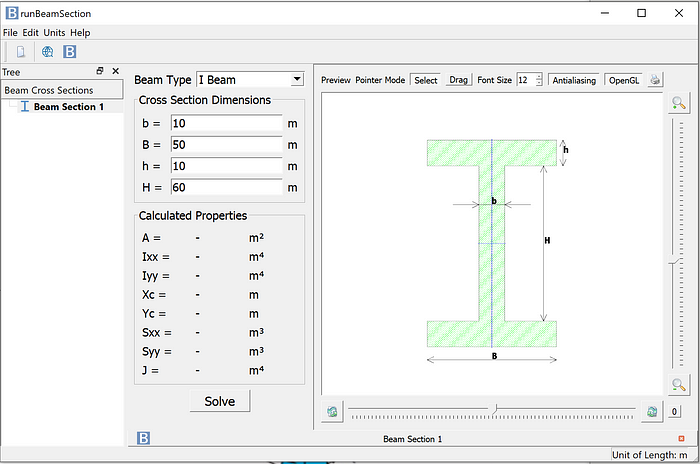
- Select the type of beam to be analyzed and calculated. Currently supported, there are I-beam, Hollow rectangle beam, Rectangle beam, C-beam, T-beam, Hollow circle beam, Round bar, and Angle beam.
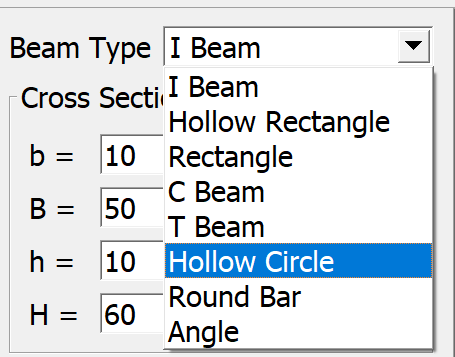
-
Set the unit of the system and enter the dimensions. While inputting the dimensions, the graph area will display the cross-sectional size and update the shape according to the input values.
-
Click the Solve button to calculate the attribute values. The supported values are cross-sectional area, the moment of inertia, the centroid distance in the x- and y-axis, elastic section modulus, and torsion constant.
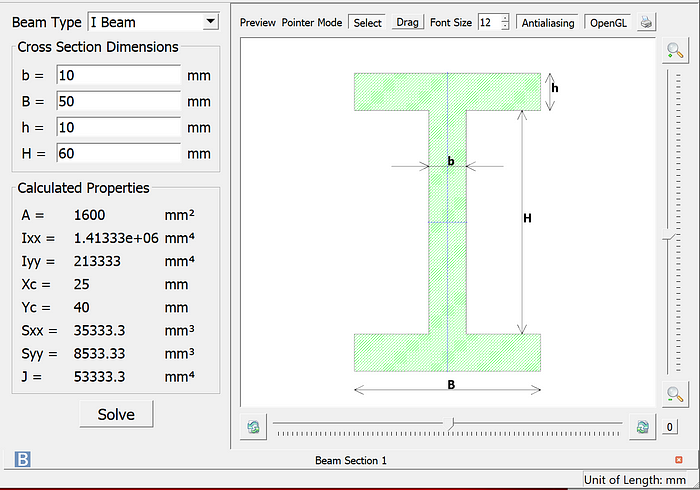
A detailed video demonstration is given here.